แหล่งพลังงานและการแผ่รังสี

แหล่งพลังงานและการแผ่รังสี

แหล่งพลังงานและการแผ่รังสี (Energy Sources and Radiation)

แสงหรือรังสีแม่เหล็กไฟฟ้า (electromagnetic radiation) ถือเป็นหนึ่งในรูปแบบของพลังงานที่สำคัญในระบบรีโมทเซนซิง โดยสามารถอธิบายได้ผ่าน สองแนวคิดหลักทางฟิสิกส์ ได้แก่ ทฤษฎีคลื่น (Wave Theory) และทฤษฎีอนุภาค (Particle Theory) ซึ่งต่างมีบทบาทสำคัญในการอธิบายพฤติกรรมของการแผ่รังสีจากวัตถุต่าง ๆ บนพื้นผิวโลก

จาก แนวคิดเชิงอนุภาค (Particle Theory) พลังงานแม่เหล็กไฟฟ้าไม่ได้แผ่ออกมาอย่างต่อเนื่อง หากแต่กระจายออกเป็นหน่วยย่อยที่เรียกว่า โฟตอน (Photon) หรือ ควอนต้า (Quantum) โดยพลังงานของแต่ละโฟตอนนั้น แปรผันตรงกับความถี่ของคลื่นแม่เหล็กไฟฟ้า ซึ่งสามารถคำนวณได้จากสมการของ Planck ดังนี้: E=hf\boxed{E = hf}E=hf​

โดยที่
E = พลังงานของ 1 โฟตอน (หน่วย: จูล, J)
h = ค่าคงที่ของพลังค์ (Planck’s Constant) มีค่าเท่ากับ 6.626×10−34 J\cdotps6.626 \times 10^{-34} \ \text{J·s}6.626×10−34 J\cdotps
f = ความถี่ของคลื่น (หน่วย: เฮิรตซ์, Hz)

หากต้องการคำนวณพลังงานโดยใช้ความยาวคลื่น (λ)(\lambda)(λ) แทนค่าความถี่ สมการสามารถเขียนใหม่ได้เป็น: E=hcλ\boxed{E = \frac{hc}{\lambda}}E=λhc​​

โดยที่
c = ความเร็วของแสงในสุญญากาศ มีค่าประมาณ 3×108 m/s3 \times 10^8 \ \text{m/s}3×108 m/s
λ = ความยาวคลื่น (หน่วย: เมตร, m)

สมการนี้แสดงให้เห็นว่า พลังงานของรังสีแม่เหล็กไฟฟ้าจะเพิ่มขึ้นเมื่อความยาวคลื่นลดลง ซึ่งเป็นหลักการสำคัญที่ใช้อธิบายความสัมพันธ์ระหว่างช่วงคลื่นต่าง ๆ กับปริมาณพลังงานที่ตรวจจับได้ผ่านเซนเซอร์ในระบบรีโมทเซนซิง

การแผ่รังสีของพลังงานจากวัตถุ

(Radiative Emission of Energy from Objects)

ในการสำรวจข้อมูลจากระยะไกล (Remote Sensing) พลังงานแม่เหล็กไฟฟ้าที่เปล่งออกมาจากพื้นผิววัตถุมีความสำคัญอย่างยิ่ง โดยเฉพาะช่วงคลื่นที่วัตถุแผ่ออกซึ่งสัมพันธ์กับอุณหภูมิพื้นผิวตามหลักการของ กฎสเตฟาน–โบลต์ซมานน์ (Stefan–Boltzmann Law)

จากหลักการทางฟิสิกส์ พลังงานที่แผ่ออกจากวัตถุมีความสัมพันธ์ผกผันกับความยาวคลื่น กล่าวคือ คลื่นที่มีความยาวมาก (เช่น ไมโครเวฟ) จะมีพลังงานต่ำ และตรวจจับได้ยากกว่าคลื่นที่มีความยาวสั้น เช่น รังสีอินฟราเรดหรือคลื่นแสงที่ตามองเห็นได้ ดังนั้น การตรวจวัดคลื่นช่วงยาวต้องอาศัยพื้นที่กว้างและเวลารวบรวมข้อมูลที่นานขึ้นเพื่อให้ได้ค่าพลังงานที่เพียงพอ

อย่างไรก็ตาม แหล่งพลังงานที่สำคัญที่สุดในระบบรีโมทเซนซิงคือดวงอาทิตย์ ซึ่งเป็นต้นกำเนิดของรังสีแม่เหล็กไฟฟ้าในช่วงคลื่นต่าง ๆ ตั้งแต่รังสีอัลตราไวโอเลตไปจนถึงอินฟราเรด และสามารถใช้ในการวิเคราะห์วัตถุต่าง ๆ บนพื้นโลกได้อย่างหลากหลาย นอกจากดวงอาทิตย์แล้ว วัตถุทุกชนิดที่มีอุณหภูมิสูงกว่า 0 องศาเคลวิน (K) หรือ −273 องศาเซลเซียส (°C) ก็สามารถแผ่รังสีแม่เหล็กไฟฟ้าออกมาได้เช่นกัน

ปริมาณพลังงานทั้งหมดที่แผ่ออกจากวัตถุขึ้นอยู่กับ อุณหภูมิพื้นผิวของวัตถุนั้น โดยมีความสัมพันธ์ตามสมการของ Stefan–Boltzmann ดังนี้: W=σT4\boxed{W = \sigma T^4}W=σT4​

โดยที่
W = พลังงานที่แผ่จากพื้นผิววัตถุต่อหน่วยพื้นที่ (หน่วย: W·m⁻²)
T = อุณหภูมิสัมบูรณ์ของวัตถุ (หน่วย: องศาเคลวิน, K)
σ = ค่าคงที่ของสเตฟาน–โบลต์ซมานน์ มีค่าเท่ากับ σ=5.6697×10−8 W\cdotpm−2\cdotpK−4\boxed{\sigma = 5.6697 \times 10^{-8} \ \text{W·m}^{-2}\text{·K}^{-4}}σ=5.6697×10−8 W\cdotpm−2\cdotpK−4​

สมการนี้ชี้ให้เห็นว่า อุณหภูมิของวัตถุมีผลโดยตรงต่อปริมาณพลังงานที่แผ่ออก และสามารถใช้เป็นตัวแปรหลักในการวิเคราะห์ความร้อนของพื้นผิวในงานด้านสิ่งแวดล้อม การเกษตร หรืออุตุนิยมวิทยา ซึ่งเป็นการนำทฤษฎีฟิสิกส์มาใช้ในเชิงประยุกต์กับระบบสารสนเทศภูมิศาสตร์และรีโมทเซนซิงได้อย่างมีประสิทธิภาพ

การแผ่พลังงานของเทหวัตถุสีดำและกฎของแพลงค์

(Blackbody Radiation and Planck’s Law)

การแผ่พลังงานของวัตถุในธรรมชาติสัมพันธ์โดยตรงกับอุณหภูมิของวัตถุนั้น และเป็นไปตาม กฎของสเตฟาน–โบลต์ซมานน์ (Stefan–Boltzmann Law) ซึ่งได้แสดงไว้ก่อนหน้านี้ว่า พลังงานรวมที่แผ่ออกจากวัตถุจะแปรผันตามอุณหภูมิสัมบูรณ์ยกกำลังสี่ (T⁴)

ในเชิงทฤษฎี พฤติกรรมของการแผ่พลังงานจะสมบูรณ์ที่สุดเมื่อพิจารณาวัตถุที่เป็น เทหวัตถุสีดำ (Black Body) ซึ่งหมายถึงวัตถุในอุดมคติที่สามารถดูดกลืนพลังงานแม่เหล็กไฟฟ้าได้ทั้งหมดที่ตกกระทบโดยไม่สะท้อนกลับ และแผ่พลังงานได้สูงสุดตามแต่ละอุณหภูมิ อย่างไรก็ตาม ในความเป็นจริง ยังไม่มีสสารใดที่มีคุณสมบัติเช่นนั้นโดยสมบูรณ์ แต่สามารถมีวัตถุที่มีพฤติกรรมใกล้เคียง เช่น ผิวของดาวฤกษ์หรือเตาแผ่รังสีบางประเภท

พลังงานที่แผ่จากเทหวัตถุสีดำต่อหนึ่งหน่วยพื้นที่สำหรับแต่ละค่าความยาวคลื่นที่กำหนด สามารถคำนวณได้จาก กฎของแพลงค์ (Planck’s Radiation Law) ซึ่งมีสมการดังนี้: Wλ=C1λ−5exp⁡(C2λT)−1\boxed{W_\lambda = \frac{C_1 \lambda^{-5}}{\exp\left(\frac{C_2}{\lambda T}\right) – 1}}Wλ​=exp(λTC2​​)−1C1​λ−5​​

โดยที่:

• Wλ\mathbf{W_\lambda}Wλ​ = พลังงานที่แผ่ออกที่ความยาวคลื่น λ\lambdaλ (หน่วย: W·m⁻²·µm⁻¹)
• λ\mathbf{\lambda}λ = ความยาวคลื่นของรังสี (หน่วย: เมตร, m)
• T\mathbf{T}T = อุณหภูมิสัมบูรณ์ของวัตถุ (หน่วย: เคลวิน, K)
• C1\mathbf{C_1}C1​ = ค่าคงที่ของแพลงค์-1, มีค่าเท่ากับ 3.74×10−16 W\cdotpm23.74 \times 10^{-16} \ \text{W·m}^23.74×10−16 W\cdotpm2
• C2\mathbf{C_2}C2​ = ค่าคงที่ของแพลงค์-2, มีค่าเท่ากับ 1.44×10−2 m\cdotpK1.44 \times 10^{-2} \ \text{m·K}1.44×10−2 m\cdotpK

สมการข้างต้นแสดงให้เห็นว่า พลังงานที่แผ่ออกมาจากวัตถุขึ้นอยู่กับทั้งอุณหภูมิของวัตถุและความยาวคลื่นของรังสีที่แผ่ออกมา กล่าวคือ เมื่ออุณหภูมิเพิ่มสูงขึ้น วัตถุจะสามารถแผ่พลังงานในช่วงคลื่นที่สั้นลง และมีปริมาณมากขึ้นได้ ซึ่งถือเป็นหลักสำคัญในการศึกษาวัตถุจากระยะไกล เช่น การวิเคราะห์พลังงานความร้อนจากผิวโลก หรือการวัดรังสีจากชั้นบรรยากาศ

กฎการแทนที่ของวีเยน (Wien’s Displacement Law)

จากทฤษฎีการแผ่รังสีของวัตถุ สามารถแสดงให้เห็นว่า ความยาวคลื่นที่ให้พลังงานการแผ่สูงสุดของเทหวัตถุสีดำ (Black Body) จะมีความสัมพันธ์ผกผันกับอุณหภูมิสัมบูรณ์ของวัตถุนั้น โดยแสดงในรูปของสมการ: λmax=CT\boxed{\lambda_{\text{max}} = \frac{C}{T}}λmax​=TC​​

โดยที่

• λmax\lambda_{\text{max}}λmax​ = ความยาวคลื่นที่ให้การแผ่พลังงานสูงสุด (เมตร)
• CCC = ค่าคงที่ของวีเยน (Wien’s Constant) มีค่าเท่ากับ 2.898×10−3 m\cdotpK2.898 \times 10^{-3} \ \text{m·K}2.898×10−3 m\cdotpK
• TTT = อุณหภูมิสัมบูรณ์ของวัตถุ (เคลวิน, K)

สมการนี้ชี้ให้เห็นว่าเมื่ออุณหภูมิของวัตถุเพิ่มสูงขึ้น ความยาวคลื่นที่แผ่พลังงานมากที่สุดจะสั้นลง กล่าวคือ วัตถุที่ร้อนกว่าจะปล่อยรังสีในช่วงคลื่นสั้น เช่น อินฟราเรดหรือแสงที่ตามองเห็น ขณะที่วัตถุที่เย็นกว่าจะปล่อยพลังงานในช่วงคลื่นที่ยาวกว่า เช่น คลื่นไมโครเวฟ

การประยุกต์ใช้กฎนี้มีความสำคัญในงานรีโมทเซนซิง เช่น การวิเคราะห์อุณหภูมิผิวโลก หรือการตรวจสอบวัตถุจากระยะไกลด้วยการเลือกช่วงคลื่นที่เหมาะสมกับอุณหภูมิเป้าหมายที่ต้องการวัด ซึ่งช่วยให้สามารถเลือกเซนเซอร์และระบบตรวจวัดได้อย่างมีประสิทธิภาพ

การแผ่รังสีของวัตถุตามอุณหภูมิ: ความสัมพันธ์กับช่วงคลื่น

จากสมการของกฎการแทนที่ของวีเยน (Wien’s Displacement Law) สามารถอนุมานได้ว่า วัตถุที่มีอุณหภูมิประมาณ 300 เคลวิน (°K) ซึ่งใกล้เคียงกับ อุณหภูมิผิวพื้นโลก จะมีการแผ่พลังงานสูงสุดที่ ช่วงคลื่นประมาณ 9.7 ไมโครเมตร ซึ่งอยู่ในบริเวณของ อินฟราเรดความร้อน (Thermal Infrared)

รังสีความร้อนในช่วงนี้ ไม่สามารถตรวจจับได้ด้วยอุปกรณ์ถ่ายภาพทั่วไป แต่ต้องใช้อุปกรณ์เฉพาะ เช่น Radiometer หรือ Thermal Scanner ที่สามารถวัดพลังงานในช่วงคลื่นยาวดังกล่าวได้อย่างแม่นยำ โดยรังสีที่แผ่ออกมาจะมีความสัมพันธ์โดยตรงกับระดับพลังงานความร้อนของผิววัตถุ ซึ่งเหมาะอย่างยิ่งในการประยุกต์ใช้เพื่อการตรวจสอบอุณหภูมิและพลังงานของพื้นผิวโลกผ่านการสำรวจระยะไกล (Remote Sensing)

ในทางกลับกัน ดวงอาทิตย์ ซึ่งมีอุณหภูมิพื้นผิวสูงกว่ามาก แผ่พลังงานสูงสุดที่ ช่วงคลื่นประมาณ 0.5 ไมโครเมตร ซึ่งอยู่ในย่าน แสงที่ตามนุษย์มองเห็นได้ (Visible spectrum) โดยเฉพาะบริเวณ แสงสีเขียว (Green Band) ช่วงคลื่นดังกล่าวสามารถตรวจจับได้ทั้งโดย ตาคน และ ฟิล์มถ่ายภาพธรรมดา รวมถึง เซนเซอร์ออปติคัล ที่ใช้ในระบบรีโมทเซนซิงชนิดพาสซีฟ

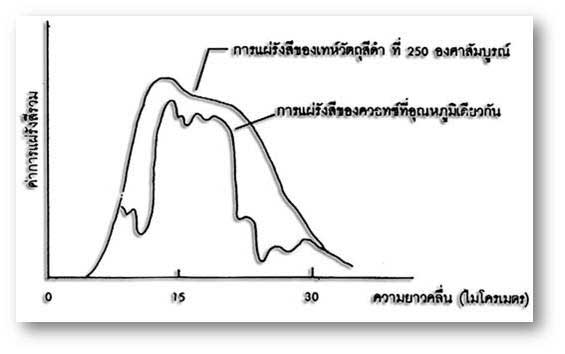
จากกราฟประกอบ (ภาพด้านบน) จะเห็นว่า เทหวัตถุสีดำที่อุณหภูมิ 250 °K มีการแผ่รังสีสูงสุดใกล้ค่าดังกล่าว โดยกราฟของวัตถุที่มีอุณหภูมิจริงจะมีลักษณะไม่เรียบเท่ากับเส้นทฤษฎี ทั้งนี้เนื่องจากปัจจัยต่าง ๆ เช่น องค์ประกอบพื้นผิว คุณสมบัติการแผ่รังสี และบรรยากาศที่มีผลต่อการแพร่กระจายของคลื่นแม่เหล็กไฟฟ้า